Форма квадрат: Квадратичная форма — Википедия – Форма ногтей Мягкий квадрат: как сделать овально-квадратный маникюр — Вместе

Содержание

Квадратичная форма — Википедия

Материал из Википедии — свободной энциклопедии

Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.

Пусть L{\displaystyle L} есть векторное пространство над полем K{\displaystyle K} и e1,e2,…,en{\displaystyle e_{1},e_{2},\dots ,e_{n}} — базис в L{\displaystyle L}.

Функция Q:L→K{\displaystyle Q:L\to K} называется квадратичной формой, если её можно представить в виде

Q(x)=∑i,j=1naijxixj,{\displaystyle Q(x)=\sum _{i,j=1}^{n}a_{ij}x_{i}x_{j},}

где x=x1e1+x2e2+⋯+xnen{\displaystyle x=x_{1}e_{1}+x_{2}e_{2}+\cdots +x_{n}e_{n}}, а aij{\displaystyle a_{ij}} — некоторые элементы поля K{\displaystyle K}.

Матрицу A=(aij){\displaystyle A=(a_{ij})} называют матрицей квадратичной формы Q(x){\displaystyle Q(x)} в данном базисе. В случае, если характеристика поля K{\displaystyle K} не равна 2, можно считать, что матрица квадратичной формы симметрична, то есть aij=aji{\displaystyle a_{ij}=a_{ji}}. Так, например, квадратичную форму от двух переменных обычно записывают в виде

Q(x1,x2)=a11x12+2a12x1x2+a22x22{\displaystyle Q(x_{1},x_{2})=a_{11}x_{1}^{2}+2a_{12}x_{1}x_{2}+a_{22}x_{2}^{2}}.

При замене базиса (т.е. невырожденной линейной замене переменных x1,…,xn{\displaystyle x_{1},\ldots ,x_{n}}) с матрицей замены C{\displaystyle C} матрица квадратичной формы изменяется по формуле

A′=CTAC,{\displaystyle A’=C^{T}A\,C,}

где A′{\displaystyle A’} — матрица квадратичной формы в новом базисе.

Из формулы A′=CTAC{\displaystyle A’=C^{T}A\,C} следует, что определитель матрицы квадратичной формы не является её инвариантом (т.е. не сохраняется при замене базиса, в отличие, например, от матрицы линейного отображения), но её ранг — является. Таким образом, определено понятие ранга квадратичной формы.
Если матрица квадратичной формы имеет полный ранг n{\displaystyle n}, то квадратичную форму называют невырожденной, в противном случае — вырожденной.
Для любой квадратичной формы Q{\displaystyle Q} существует единственная симметричная билинейная форма B{\displaystyle B}, такая, что Q(x)=B(x,x){\displaystyle Q(x)=B(x,x)}. Билинейную форму B{\displaystyle B} называют полярной к Q{\displaystyle Q}, она может быть вычислена по формуле

B(x,y)=12(Q(x+y)−Q(x)−Q(y)).{\displaystyle B(x,y)={\frac {1}{2}}\,(Q(x+y)-Q(x)-Q(y)).}

Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.

Знакоопределённые и знакопеременные формы[править | править код]

В случае, когда K=R{\displaystyle K=\mathbb {R} } (поле вещественных чисел), важную роль, в том числе, для различных приложений, играют понятия положительно и отрицательно определённой квадратичной формы.

Для решения вопроса о том, является ли данная квадратичная форма положительно (отрицательно) определённой, используется критерий Сильвестра:

Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.

Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения.

Вещественный случай[править | править код]

В случае, когда K=R{\displaystyle K=\mathbb {R} } (поле вещественных чисел), для любой квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет

канонический вид (нормальный вид):

Q(x)=x12+⋯+xp2−xp+12−⋯−xp+q2, 0≤p,q≤r,p+q=r,(∗){\displaystyle Q(x)=x_{1}^{2}+\cdots +x_{p}^{2}-x_{p+1}^{2}-\cdots -x_{p+q}^{2},\quad \ 0\leq p,q\leq r,\quad p+q=r,\qquad (*)}

где r{\displaystyle r} — ранг квадратичной формы. В случае невырожденной квадратичной формы p+q=n{\displaystyle p+q=n}, а в случае вырожденной — p+q<n{\displaystyle p+q<n}.

Для приведения квадратичной формы к каноническому виду обычно используются метод Лагранжа или ортогональные преобразования базиса, причем привести данную квадратичную форму к каноническому виду можно не одним, а многими способами.

Число q{\displaystyle q} (отрицательных членов) называется индексом инерции данной квадратичной формы, а число p−q{\displaystyle p-q} (разность между числом положительных и отрицательных членов) называется сигнатурой квадратичной формы. Отметим, что иногда сигнатурой квадратичной формы называют пару (p,q){\displaystyle (p,q)}. Числа p,q,p−q{\displaystyle p,q,p-q} являются инвариантами квадратичной формы, т.е. не зависят от способа её приведения к каноническому виду (закон инерции Сильвестра).

Комплексный случай[править | править код]

В случае, когда K=C{\displaystyle K=\mathbb {C} } (поле комплексных чисел), для любой квадратичной формы существует базис, в котором форма имеет канонический вид

Q(x)=x12+⋯+xr2,(∗∗){\displaystyle Q(x)=x_{1}^{2}+\cdots +x_{r}^{2},\qquad (**)}

где r{\displaystyle r} — ранг квадратичной формы. Таким образом, в комплексном случае (в отличие от вещественного) квадратичная форма имеет один единственный инвариант — ранг, и все невырожденные формы имеют один и тот же канонический вид (сумма квадратов).

Беклемишев Д. В. Аналитическая геометрия и линейная алгебра.-М.: Высш. шк. 1998, 320с.
Гельфанд И. М., Линейная алгебра. Курс лекций.
Гельфанд И. М. Лекции по линейной алгебре М.: Наука, 1971.
* Конвей Дж. Квадратичные формы, данные нам в ощущениях. — М.: МЦНМО, 2008. — 144 с. — 1000 экз. — ISBN 978-5-94057-268-8.
Мальцев А. И. Основы линейной алгебры. М.: Наука, 1975.
Фаддеев Д. К. Лекции по алгебре. М.: Наука, 1984.
Кострикин А. И. Введение в алгебру, М.: Наука, 1977.
Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.

Квадратичные формы

Квадратичной формойf(х₁, х₂,…,х_n) от n переменных называют сумму, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятым с некоторым коэффициентом:f(х₁, х₂,…,х_n) =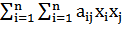(a_ij=a_ji).

Матрицу А, составленную из этих коэффициентов, называют матрицей квадратичной формы. Это всегда симметрическаяматрица (т.е. матрица, симметричная относительно главной диагонали,a_ij=a_ji).

В матричной записи квадратичная форма имеет вид f(Х) = Х^ТAX, где

. В самом деле

Например, запишем в матричном виде квадратичную форму .

Для этого найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, а остальные элементы — половинам соответствующих коэффициентов квадратичной формы. Поэтому

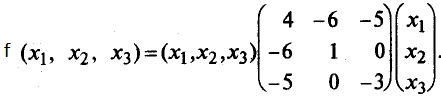
Пусть матрица-столбец переменных X получена невырожденным линейным преобразовании матрицы-столбца Y, т.е. X = CY, где С — невырожденная матрица n-го порядка. Тогда квадратичная форма f(X) = Х^TАХ = (CY)^TA(CY) = (Y^TC^T)A(CY) =Y^T(C^TAC)Y.

Таким образом, при невырожденном линейном преобразовании С матрица квадратичной формы принимает вид: А

*=C^TAC.

Например, найдем квадратичную форму f(y₁, y₂), полученную из квадратичной формыf(х₁, х₂) = 2x₁²+ 4х₁х₂— 3х₂²линейным преобразованием .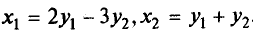

Квадратичная форма называется канонической(имеетканонический вид), если все ее коэффициентыa_ij= 0 приi≠j, т.е.f(х₁, х₂,…,х_n) = a₁₁ x₁² + a₂₂ x₂²+ … + a_nn x_n² = .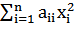

Ее матрица является диагональной.

Теорема(доказательство здесь не приводится). Любая квадратичная форма может быть приведена к каноническому виду с помощью невырожденного линейного преобразования.

Например, приведем к каноническому виду квадратичную форму f(х₁, х₂,х₃) = 2x₁²+ 4х₁х₂— 3х₂²– х₂х₃.

Для этого вначале выделим полный квадрат при переменной х₁:

f(х₁, х₂, х₃) = 2(x₁²+ 2х₁х₂+ х₂²) — 2х₂²— 3х₂²– х₂х₃= 2(x₁+ х₂)²— 5х₂²– х₂х₃.

Теперь выделяем полный квадрат при переменной х₂:

f(х₁, х₂, х₃) = 2(x₁+ х₂)²– 5(х₂²

– 2* х₂*(1/10)х₃+ (1/100)х₃²) — (5/100)х₃²= = 2(x₁+ х₂)²– 5(х₂– (1/10)х₃)²— (1/20)х₃².

Тогда невырожденное линейное преобразование y₁= x₁+ х₂,y₂= х₂– (1/10)х₃иy₃= x₃приводит данную квадратичную форму к каноническому видуf(y₁,y₂,y₃) = 2y₁²— 5y₂²— (1/20)y₃².

Отметим, что канонический вид квадратичной формы определяется неоднозначно (одна и та же квадратичная форма может быть приведена к каноническому виду разными способами^¹). Однако полученные различными способами канонические формы обладают рядом общих свойств. В частности, число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду (например, в рассмотренном примере всегда будет два отрицательных и один положительный коэффициент). Это свойство называют

законом инерции квадратичных форм.

Убедимся в этом, по-другому приведя ту же квадратичную форму к каноническому виду. Начнем преобразование с переменной х₂:f(х₁, х₂,х₃) = 2x₁²+ 4х₁х₂— 3х₂²– х₂х₃= -3х₂²– х₂х₃+ 4х₁х₂+ 2x₁²= -3(х₂²– — 2* х₂((1/6) х₃+ (2/3)х₁) +((1/6) х₃+ (2/3)х₁)²) – 3((1/6) х₃+ (2/3)х₁)²+ 2x₁²= = -3(х₂– (1/6) х₃— (2/3)х₁)²– 3((1/6) х₃+ (2/3)х₁)

2+ 2x₁²=f(y₁,y₂,y₃) = -3y₁²— -3y₂²+ 2y₃², гдеy₁= — (2/3)х₁+ х₂– (1/6) х₃,y₂= (2/3)х₁+ (1/6) х₃иy₃= x₁. Здесь положительный коэффициент 2 приy₃и два отрицательных коэффициента (-3) приy₁иy₂(а при использовании другого способа мы получили положительный коэффициент 2 приy₁и два отрицательных – (-5) приy₂и (-1/20) приy₃).

Также следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.

Квадратичную форму f(X) называютположительно(отрицательно)определенной, если при всех значениях переменных, не равных одновременно нулю, она положительна, т.е.f(X) > 0 (отрицательна, т.е.f(X) < 0).

Например, квадратичная форма f₁(X) = x₁²+ х₂²— положительно определенная, т.к. представляет собой сумму квадратов, а квадратичная формаf₂(X) = -x₁²+ 2x₁х₂— х₂²— отрицательно определенная, т.к. представляет ее можно представить в видеf₂(X) = -(x₁— х₂)².

В большинстве практических ситуации установить знакоопределенность квадратичной формы несколько сложнее, поэтому для этого используют одну из следующих теорем (сформулируем их без доказательств).

Теорема. Квадратичная форма является положительно (отрицательно) определенной тогда и только тогда, когда все собственные значения ее матрицы положительны (отрицательны).

Теорема (критерий Сильвестра). Квадратичная форма является положительно определенной тогда и только тогда, когда все главные миноры матрицы этой формы положительны.

Главным (угловым) миноромk-го порядка матрицы Аn-го порядка называют определитель матрицы, составленный из первыхkстрок и столбцов матрицы А ().

Отметим, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, причем минор первого порядка должен быть отрицательным.

Например, исследуем на знакоопределенность квадратичную форму f(х₁, х₂) = 2x₁²+ 4х₁х₂+ 3х₂².

Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид= (2 -)* *(3 -) – 4 = (6 — 2- 3+

2) – 4 =²— 5+ 2 = 0;D= 25 – 8 = 17;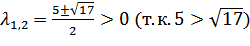. Следовательно, квадратичная форма – положительно определенная.

Способ 2. Главный минор первого порядка матрицы А ₁=a₁₁= 2 > 0. Главный минор второго порядка₂=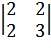= 6 – 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма – положительно определенная.

Исследуем на знакоопределенность другую квадратичную форму, f(х₁, х₂) = -2x₁²+ 4х₁х₂— 3х₂².

Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид

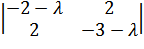
= (-2 -)* *(-3 -) – 4 = (6 + 2+ 3+²) – 4 =²+ 5+ 2 = 0;D= 25 – 8 = 17;. Следовательно, квадратичная форма – отрицательно определенная.

Способ 2. Главный минор первого порядка матрицы А ₁=a₁₁= = -2 < 0. Главный минор второго порядка₂== 6 – 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма – отрицательно определенная (знаки главных миноров чередуются, начиная с минуса).

И в качестве еще одного примера исследуем на знакоопределенность квадратичную форму f(х₁, х₂) = 2x₁²+ 4х₁х₂— 3х₂².

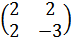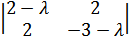Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид= (2 -)* *(-3 -) – 4 = (-6 — 2+ 3+²) – 4 =²+- 10 = 0;D= 1 + 40 = 41;. Одно из этих чисел отрицательно, а другое – положительно. Знаки собственных значений разные. Следовательно, квадратичная форма не может быть ни отрицательно, ни положительно определенной, т.е. эта квадратичная форма не является знакоопределенной (может принимать значения любого знака).

Способ 2. Главный минор первого порядка матрицы А ₁=a₁₁= 2 > 0. Главный минор второго порядка₂=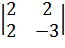= -6 – 4 = -10 < 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них – положителен).

1Рассмотренный способ приведения квадратичной формы к каноническому виду удобно использовать, когда при квадратах переменных встречаются ненулевые коэффициенты. Если их нет, осуществить преобразование все равно возможно, но приходится использовать некоторые другие приемы. Например, пустьf(х₁, х₂) = 2x₁х₂= x₁²+ 2x₁х₂+ х₂²— x₁²— х₂²=

= (x₁+ х₂)²— x₁²— х₂²= (x₁+ х₂)²– (x₁²— 2x₁х₂+ х₂²) — 2x₁х₂= (x₁+ х₂)²– — (x₁— х₂)²— 2x₁х₂; 4x₁х₂= (x₁+ х₂)²– (x₁— х₂)²;f(х₁, х₂) = 2x₁х₂= (1/2)* *(x₁+ х₂)²– (1/2)*(x₁— х₂)²=f(y₁,y₂) = (1/2)y₁²– (1/2)y₂², гдеy₁= х₁+ х₂, аy₂= х₁– х₂.

ФОРМА КВАДРАТ НА НАТУРАЛЬНЫХ НОГТЯХ

В этой статье я вам расскажу, как придать натуральным ногтям квадратную форму, форму мягкий квадрат и квадрат с закругленными краями. Объясню отличия этих форм и нюансы опила.

Для того, чтобы подпилить натуральный ноготь, с ногтевой пластины должно быть снято искусственное покрытие. Для опила мне понадобится пилочка 100/180 грит, у меня она тоненькая на деревянной основе.

Шаг 1. Возьму в руки пилку удобным для меня захватом. Большой палец у меня находится с одной стороны, а четыре остальных с другой.

Шаг 2. Сначала я подпилю ноготь с двух боков. Пилку необходимо держать перпендикулярно относительно натурального ногтя и опиливать только свободный край, иначе можно истончить и повредить боковые части натурального ногтя. Хочу обратить внимание, что подпиливать боковые части нужно таким образом, чтобы точка выхода ногтевой пластины была ровной и при отрастании ногтя не было ступеней между опиленным краем и отросшим.

Правильная постановка пилки для опила натурального ногтя

Неправильная постановка пилки. Применяется для опила искусственного ногтя

Шаг 3. Теперь я подпилю торцевую часть ногтевой пластины.

Для придания ногтю формы квадрат, пилку я держу строго перпендикулярно ногтевой пластине. Чтобы уголки не кололись и не мешали, я их слегка подпилю мягкой стороной пилки (буквально пару движений).

Для придания формы мягкий квадрат необходимо у квадрата спилить углы. Для этого я подставляю пилку под углом к ногтевой пластине и подпилю уголки.

Для придания формы ногтя квадрат с закругленными углами необходимо у квадрата закруглить углы.

Шаг 4. После подпиливания ногтевой пластины, обратной стороной пушера я прочищаю под ногтем и убираю остатки опила, иначе в дальнейшем могут появиться отслойки гель-лака.

Шаг 5. Теперь мягкой стороной пилки я зашлифовываю торец и окончательно убираю остатки опила.

Работа по подпиливанию ногтевых пластин окончена.

С вами была Ирина Набок.

До новых встреч.

Читайте также:

Полезные ссылки:

◉ Акригель LadyMistry 30 ml ► http://ali.pub/29s7l4
◉ Акригель LadyMistry 60 ml ► http://ali.pub/29s7t3
◉ Акригель MSHARE ► http://ali.pub/27tlxe ► http://got.by/27tlxe
◉ Кисть для Акригеля ► http://ali.pub/27tm47 ► http://got.by/27tm47
◉ Гель Лаки Fiore > https://vk.cc/7jSgYo
◉ Мебель маникюр (Подставка под руку, столы) https://vk.com/mebel_manikur и инстаграм @mebel_manikur Скидка 10% по купону GRANDNAIL
◉ Магазин Евромедсервис: Аппараты для маникюра и педикюра http://bit.ly/21onYVm
Магазин предоставил скидку моим подписчикам 15% ПРОМОКОД GRAND15
◉ Лампы Sun в магазине, где покупаю я > http://ali.pub/mc8hn

Оцените статью и спрашивайте, если остались вопросы

comments powered by HyperComments

Новые Курсы Ирины Набок

Наращивание и Коррекция на Верхние Формы Акригелем с правильной конструкцией

от 4 900 руб

Работа колпачками в маникюре Мини курс

3500руб

990 руб

Онлайн Курсы GRAND NAIL

Современный Гель лак

15700руб

7 800 руб

Курс Наращивания и Коррекции Ногтей Акригелем (Полигелем)

29500руб

17 500 руб

Базовые знания о материалах для покрытия и наращивания ногтей 2019
Видео-семинар Ирины Набок

1 200 руб

Онлайн Практикумы — GRAND NAIL

Новая технология укрепления натуральных ногтей

от 4 000 РУБ

Наращивание и коррекция ногтей Акригелем Квадрат

от 4000 РУБ

Наращивание и коррекция ногтей Акригелем Овал

от 4000 РУБ

Без опила. Техника работы с твердыми материалами

от 4000 РУБ

Выкладной Френч Акригель

от 4000 РУБ

Исправление Клювовидных или Внизрастущих ногтей

1790 РУБ

Онлайн Курсы Дизайна Ногтей — GRAND NAIL

MAGIC FLOWERS
Курс дизайна ногтей

от 3 000 руб

АКВАРЕЛЬ
Курс дизайна ногтей

от 3 000 руб

DREAM WHITE
Курс дизайна ногтей

от 3 000 руб

ЮВЕЛИРНЫЙ
Курс дизайна ногтей

от 3 000 руб

КРУЖЕВНЫЕ ФАНТАЗИИ
Курс дизайна ногтей

от 3 000 руб

АЭРОПУФФИНГ
Курс дизайна ногтей

от 3 000 руб

КУРС ИДЕАЛЬНЫЕ ВЕНЗЕЛЯ
7000руб

4 900 руб

Закрытая группа
Дизайна ногтей Юлии Матюхиной

990 руб/месяц

Курсы по санитарной безопасности

БЕЗОПАСНЫЙ МАНИКЮР 2.0
КУРС О ЗАБОЛЕВАНИЯХ НОГТЕЙ, КОЖИ КИСТЕЙ И СТОП

от 3000 РУБ

Квадратичная форма — это… Что такое Квадратичная форма?

Определение

Пусть есть векторное пространство над полем и — базис в .

Функция называется квадратичной формой, если её можно представить в виде

где , а — некоторые элементы поля .

Связанные определения

Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.

Эквивалентные квадратичные формы

Две квадратичные формы и называются эквивалентными, если найдется целочисленная матрица:

с определителем равным 1, переводящая матрицу в матрицу :

Поскольку эквивалентное преобразование не меняет детерминант формы, необходимым условием эквивалентности двух форм является равенство их детерминантов. Однако обратное неверно: среди форм с одинаковым дискриминантом может найтись конечное число неэквивалентных.

Редуцированные квадратичные формы

Положим любое положительное целое число, не являющееся квадратом какого-либо другого целого числа. Каждый класс неопределенных квадратичных форм с дискриминантом содержит набор канонических представлений, называющихся редуцированными формами. Квадратичная форма называется редуцированной, если .

Так же нетрудно заметить, что квадратичная форма является редуцированной тогда и только тогда, когда и, что число редуцированных квадратичных форм определенного дискриминанта конечно.

Квадратные, смежные и неоднозначные квадратичные формы

Две формы и называются смежными, если выполняется условие , например:

Также на множестве эквивалентных форм можно определить операцию умножения(композицию) тогда, если коэффициенты и взаимно-просты,

Квадратной формой называется квадратичная форма вида , в которой третий коэффициент является полным квадратом. Из квадратичной формы можно извлечь квадратный корень. Для вычисления корня заменим форму на эквивалентную ей смежную форму , потом извлечем квадратный корень на основании предыдущего определения. В итоге операция извлечения корня сведется к следующему:

^[1]

Форма вида называется неоднозначной. Если форма неоднозначна, то ее определитель делится на

Свойства

Критерий Сильвестра
- Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
- Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.
Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения.

Для любой невырожденной квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид:
- Разность между числом положительных () и отрицательных () членов в этой записи называется сигнатурой квадратичной формы. Сигнатура, также как и числа положительных и отрицательных слагаемых, не зависят от способов приведения квадратичной формы к каноническому виду (закон инерции Сильвестра).
Для приведения квадратичной формы к каноническому виду обычно используется метод Лагранжа.

Примеры

Примечания

↑ Ш.Т. Ишмухаметов Методы факторизации натуральных чисел, Казанский университет, 2011 стр 78

Литература

Мальцев А. И. Основы линейной алгебры. М.: Наука, 1975.
Гельфанд И. М. Лекции по линейной алгебре М.: Наука, 1971.
Фаддеев Д. К. Лекции по алгебре. М.: Наука, 1984.
Кострикин А. И. Введение в алгебру, М.: Наука, 1977.
Беклемишев Д. В. Аналитическая геометрия и линейная алгебра.-М.: Высш. шк. 1998, 320с.
Гельфанд И. М., Линейная алгебра. Курс лекций.
Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.

Квадратичная форма — это… Что такое Квадратичная форма?

Определение

Пусть есть векторное пространство над полем и — базис в .

Функция называется квадратичной формой, если её можно представить в виде

где , а — некоторые элементы поля .

Связанные определения

Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.

Эквивалентные квадратичные формы

Две квадратичные формы и называются эквивалентными, если найдется целочисленная матрица:

с определителем равным 1, переводящая матрицу в матрицу :

Редуцированные квадратичные формы

Квадратные, смежные и неоднозначные квадратичные формы

Две формы и называются смежными, если выполняется условие , например:

^[1]

Форма вида называется неоднозначной. Если форма неоднозначна, то ее определитель делится на

Свойства

Критерий Сильвестра
- Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
- Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.
Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения.

Для любой невырожденной квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид:
- Разность между числом положительных () и отрицательных () членов в этой записи называется сигнатурой квадратичной формы. Сигнатура, также как и числа положительных и отрицательных слагаемых, не зависят от способов приведения квадратичной формы к каноническому виду (закон инерции Сильвестра).
Для приведения квадратичной формы к каноническому виду обычно используется метод Лагранжа.

Примеры

Примечания

↑ Ш.Т. Ишмухаметов Методы факторизации натуральных чисел, Казанский университет, 2011 стр 78

Литература

Мальцев А. И. Основы линейной алгебры. М.: Наука, 1975.
Гельфанд И. М. Лекции по линейной алгебре М.: Наука, 1971.
Фаддеев Д. К. Лекции по алгебре. М.: Наука, 1984.
Кострикин А. И. Введение в алгебру, М.: Наука, 1977.
Беклемишев Д. В. Аналитическая геометрия и линейная алгебра.-М.: Высш. шк. 1998, 320с.
Гельфанд И. М., Линейная алгебра. Курс лекций.
Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.

Первая квадратичная форма — Википедия

Материал из Википедии — свободной энциклопедии

Первая квадратичная форма (или первая фундаментальная форма или метрический тензор) поверхности ― квадратичная форма на касательном расслоении поверхности, которая определяет внутреннюю геометрию поверхности в окрестности данной точки. Первая квадратичная форма часто обозначается I{\displaystyle \mathrm {I} }.

Знание первой квадратичной формы достаточно для вычисления гауссовой кривизны поверхности, а также для вычисления длин дуг, углов между кривыми и площади областей на поверхности.

Пусть в евклидовом пространстве со скалярным произведением ⟨⋅,⋅⟩{\displaystyle \langle \cdot ,\cdot \rangle } поверхность задана уравнением r=r(u,v),{\displaystyle r=r(u,v),} где u{\displaystyle u} и v{\displaystyle v} ― внутренние координаты на поверхности; dr=rudu+rvdv{\displaystyle dr=r_{u}du+r_{v}dv} ― дифференциал радиус-вектора r{\displaystyle r} вдоль выбранного направления смещения из точки M{\displaystyle M} в бесконечно близкую точку M′{\displaystyle M’}. (Здесь ru{\displaystyle r_{u}} и rv{\displaystyle r_{v}} — частные производные радиус-вектора r{\displaystyle r} по u{\displaystyle u} и по v{\displaystyle v} соответственно.) Тогда квадрат главной части приращения длины |MM′|{\displaystyle |MM’|} выражается квадратом дифференциала dr{\displaystyle dr}:

I=(dr)2=⟨ru,ru⟩du2+2⟨ru,rv⟩dudv+⟨rv,rv⟩dv2{\displaystyle \mathrm {I} =(dr)^{2}=\langle r_{u},r_{u}\rangle du^{2}+2\langle r_{u},r_{v}\rangle dudv+\langle r_{v},r_{v}\rangle dv^{2}}

и называется первой квадратичной формой поверхности.

Коэффициенты первой квадратичной формы обычно обозначают через

E=|ru|2, F=⟨ru,rv⟩, G=|rv|2{\displaystyle E=|r_{u}|^{2},\ F=\langle r_{u},r_{v}\rangle ,\ G=|r_{v}|^{2}}

или, в тензорных символах,

I=dr2=g1,1du2+2g1,2dudv+g2,2dv2.{\displaystyle \mathrm {I} =dr^{2}=g_{1,1}du^{2}+2g_{1,2}dudv+g_{2,2}dv^{2}.}

Тензор gi,j{\displaystyle g_{i,j}} называется основным, или метрическим, тензором поверхности.

Первая квадратичная форма является положительно определенной формой в обыкновенных точках поверхности; в частности
EG−F2>0.{\displaystyle EG-F^{2}>0.}

Мищенко А.С. Фоменко А.Т. Курс дифференциальной геометрии и топологии. — Физматлит, 2004. — ISBN 5-9221-0442-X.

Топоногов В.А. Дифференциальная геометрия кривых и поверхностей. — Физматкнига, 2012. — ISBN 9785891552135.

Квадратичная форма — это… Что такое Квадратичная форма?

Определение

Пусть есть векторное пространство над полем и — базис в .

Функция называется квадратичной формой, если её можно представить в виде

где , а — некоторые элементы поля .

Связанные определения

Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.

Эквивалентные квадратичные формы

Две квадратичные формы и называются эквивалентными, если найдется целочисленная матрица:

с определителем равным 1, переводящая матрицу в матрицу :

Редуцированные квадратичные формы

Квадратные, смежные и неоднозначные квадратичные формы

Две формы и называются смежными, если выполняется условие , например:

^[1]

Форма вида называется неоднозначной. Если форма неоднозначна, то ее определитель делится на

Свойства

Критерий Сильвестра
- Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
- Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.
Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения.

Для любой невырожденной квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид:
- Разность между числом положительных () и отрицательных () членов в этой записи называется сигнатурой квадратичной формы. Сигнатура, также как и числа положительных и отрицательных слагаемых, не зависят от способов приведения квадратичной формы к каноническому виду (закон инерции Сильвестра).
Для приведения квадратичной формы к каноническому виду обычно используется метод Лагранжа.

Примеры

Примечания

↑ Ш.Т. Ишмухаметов Методы факторизации натуральных чисел, Казанский университет, 2011 стр 78

Литература

Мальцев А. И. Основы линейной алгебры. М.: Наука, 1975.
Гельфанд И. М. Лекции по линейной алгебре М.: Наука, 1971.
Фаддеев Д. К. Лекции по алгебре. М.: Наука, 1984.
Кострикин А. И. Введение в алгебру, М.: Наука, 1977.
Беклемишев Д. В. Аналитическая геометрия и линейная алгебра.-М.: Высш. шк. 1998, 320с.
Гельфанд И. М., Линейная алгебра. Курс лекций.
Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.