By: alexxlab Posted on

Градиент концентрации — Википедия

Материал из Википедии — свободной энциклопедии

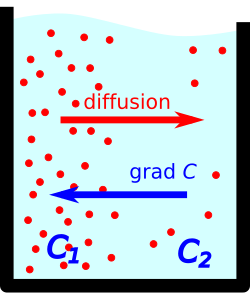При наличии градиента концентрации в растворе наблюдается диффузия — диффузионный поток растворённого вещества направлен против градиента концентрации. 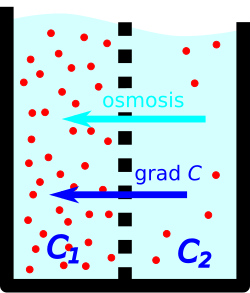Если имеется полупроницаемая перегородка, пропускающая только молекулы растворителя (но не растворённого вещества), наблюдается осмос — поток растворителя, направлен по градиенту концентрации.

Градиент концентрации или концентрационный градиент — это векторная физическая величина, характеризующая величину и направление наибольшего изменения концентрации какого-либо вещества в среде. Например, если рассмотреть две области с различной концентрацией какого-либо вещества, разделённые полупроницаемой мембраной, то градиент концентрации будет направлен

из области меньшей концентрации вещества в область с большей его концентрацией. Вектор диффузионного потока направлен против вектора градиента концентрации, что, в соответствии с принципом Ле-Шателье, приводит со временем к уменьшению этого потока и градиента концентрации.

Градиент концентрации направлен по пути l{\displaystyle l}, соответствующему нормали к изоконцентрационной поверхности (полупроницаемой мембране). Значение градиента концентрации ∇C{\displaystyle \nabla C} равно отношению приращения концентрации dC{\displaystyle dC} к соответствующему приращению пути dl{\displaystyle dl}:

∇C=dCdl.{\displaystyle \nabla C={\frac {dC}{dl}}.}

При постоянном значении градиента концентрации C{\displaystyle C} на длине пути l{\displaystyle l}:

∇C=C1−C2l.{\displaystyle \nabla C={\frac {C_{1}-C_{2}}{l}}.}

Здесь C1{\displaystyle C_{1}} и C2{\displaystyle C_{2}} — начальное и конечное значение концентрации на длине пути l{\displaystyle l} (нормали к изоконцентрационной поверхности).

Градиент концентрации может быть причиной переноса веществ, например диффузии. Диффузия осуществляется против вектора градиента концентрации[источник не указан 1219 дней].

Единицей измерения градиента концентрации в Международной системе единиц (СИ) является величина м−4 (моль/м4 или кг/м4), а также её дольные или кратные производные.

4-градиент — Википедия

Материал из Википедии — свободной энциклопедии

4-градие́нт (четыре-градиент, четырёхградиент, 4-на́бла; обозначается D, ∇μ{\displaystyle \nabla _{\mu }} или ∂μ{\displaystyle \partial _{\mu }}) в специальной теории относительности — 4-векторный дифференциальный оператор в псевдоевклидовом пространстве Минковского, определяемый как[1]

∂μ=∇μ=(∂c∂t,∇→)=(∂c∂t,∂∂x,∂∂y,∂∂z),{\displaystyle \partial _{\mu }=\nabla _{\mu }=\left({\frac {\partial }{c\,\partial t}},\;{\vec {\nabla }}\right)=\left({\frac {\partial }{c\,\partial t}},\;{\frac {\partial }{\partial x}},\;{\frac {\partial }{\partial y}},\;{\frac {\partial }{\partial z}}\;\right),}

где ∇→=(∂∂x,∂∂y,∂∂z){\displaystyle {\vec {\nabla }}=\left({\frac {\partial }{\partial x}},\;{\frac {\partial }{\partial y}},\;{\frac {\partial }{\partial z}}\;\right)} — 3-вектор градиента. Следует отметить, что выше записаны ковариантные компоненты 4-векторного оператора. Контравариантные компоненты ∂μ=∇μ=gμν∇ν=(∂c∂t,−∇→),{\displaystyle \partial ^{\mu }=\nabla ^{\mu }=g^{\mu \nu }\nabla _{\nu }=\left({\frac {\partial }{c\,\partial t}},\;-{\vec {\nabla }}\right),} отличающиеся знаком минус перед пространственными компонентами, используются редко, например для вычисления квадрата 4-градиента[1] (здесь и ниже gμν=diag(1,−1,−1,−1){\displaystyle g^{\mu \nu }=\mathrm {diag} (1,-1,-1,-1)} — метрический тензор; используется соглашение Эйнштейна о суммировании по повторяющимся координатным индексам).

Если вычислить скалярное произведение D на самого себя (учитывая, что пространство Минковского псевдоевклидово), то получится скалярный 4-мерный оператор Д’Аламбера:

◻=D⋅D=gμν∇μ∇ν=∂ν∂ν=∂2c2∂t2−Δ=∂2c2∂t2−∂2∂x2−∂2∂y2−∂2∂z2,{\displaystyle \square =D\cdot D=g^{\mu \nu }\nabla _{\mu }\nabla _{\nu }=\partial ^{\nu }\partial _{\nu }={\frac {\partial ^{2}}{c^{2}\partial t^{2}}}-\Delta ={\frac {\partial ^{2}}{c^{2}\partial t^{2}}}-{\frac {\partial ^{2}}{\partial x^{2}}}-{\frac {\partial ^{2}}{\partial y^{2}}}-{\frac {\partial ^{2}}{\partial z^{2}}}\;,}

где Δ — оператор Лапласа.

Ещё один способ обозначения 4-градиента — запятая перед координатным индексом. Так, если а — скаляр, то его 4-градиент

∂μa=a,μ.{\displaystyle \partial _{\mu }a=a_{\;,\mu }\;.}

Скалярное произведение вектора 4-градиента (слева) на 4-вектор определяет 4-дивергенцию:

D⋅A=∂μAμ=A,μμ=∂Atc∂t+∂Ax∂x+∂Ay∂y+∂Az∂z=∂Atc∂t+∇A,{\displaystyle D\cdot A=\partial _{\mu }A^{\mu }=A_{\;,\mu }^{\mu }={\frac {\partial A_{t}}{c\;\partial t}}+{\frac {\partial A_{x}}{\partial x}}+{\frac {\partial A_{y}}{\partial y}}+{\frac {\partial A_{z}}{\partial z}}={\frac {\partial A_{t}}{c\;\partial t}}+\nabla \mathbf {A} ,}

где Aμ={A0,A1,A2,A3}={At,A}{\displaystyle A^{\mu }=\{A^{0},A^{1},A^{2},A^{3}\}=\{A_{t},\mathbf {A} \}} — контравариантные компоненты 4-вектора, а ∇A{\displaystyle \nabla \mathbf {A} } — дивергенция.

Символ Dμ{\displaystyle D_{\mu }} (и иногда ∇μ{\displaystyle \nabla _{\mu }}) используется также как ковариантная производная в криволинейных координатах:

DμAν=∂μAν+ΓαμνAα,{\displaystyle D_{\mu }A^{\nu }=\partial _{\mu }A^{\nu }+\Gamma _{\alpha \mu }^{\nu }A^{\alpha },}

где Γαμν{\displaystyle \Gamma _{\alpha \mu }^{\nu }} — символы Кристоффеля. В декартовых координатах евклидового (псевдоевклидового) пространства символы Кристоффеля равны нулю и ковариантная производная совпадает с 4-градиентом. Ковариантная производная скаляра совпадает с 4-градиентом независимо от криволинейности координат:

Dμa=∂μa.{\displaystyle D_{\mu }a=\partial _{\mu }a.}
  • S. Hildebrandt, «Analysis II» (Calculus II), ISBN 3-540-43970-6, 2003.
  • L. C. Evans, «Partial differential equations», A.M.Society, Grad. Studies Vol. 19, 1988.
  • J. D. Jackson, «Classical Electrodynamics» Chapter 11, Wiley ISBN 0-471-30932-X.

Барический градиент — Википедия

Материал из Википедии — свободной энциклопедии

Бари́ческий градие́нт — в гидродинамике — вектор, характеризующий степень изменения давления сплошной среды в пространстве.

По числовой величине барический градиент равен отношению изменения давления на единицу расстояния в том направлении, в котором давление убывает наиболее быстро, то есть вектор направлен по нормали к изобарной поверхности в сторону уменьшения давления.

Вектор барического градиента равен по модулю и направлен противоположно вектору градиента давления:

Gb=−∇P=−grad P=−∂P∂nn,{\displaystyle \mathbf {G_{b}} =-\nabla P=-\mathbf {grad} \ P=-{\frac {\partial P}{\partial n}}\mathbf {n} ,}
где n{\displaystyle \mathbf {n} } — единичный вектор направленный по нормали к изобарной поверхности.

В СИ размерность барического градиента — паскаль на метр (Па/м) и совпадает с размерностью объёмной плотности силы (Н/м3).

В метеорологии различают вертикальный и горизонтальный барические градиенты. Вертикальный барический градиент — это вертикальная компонента вектора барического градиента. В метеорологии обычно пользуются горизонтальным барическим градиентом, который часто называют просто градиентом, то есть составляющей вектора барического градиента, лежащего в горизонтальной плоскости. В горизонтальной плоскости вектор горизонтального градиента нормален к линиям изобар и направлен в сторону уменьшения давления.

Горизонтальный барический градиент вычисляют по атмосферному давлению приведённому к некоторому оговорённому уровню, обычно к уровню моря. В метеорологии эту величину обычно выражают в барах на 100 км.

Модуль вертикального барического градиента много больше модуля вертикального барического градиента, так как атмосферное давление довольно быстро падает с увеличением высоты. Иногда в метеорологии и в барометрическом нивелировании применяется другая величина для характеристики падения атмосферного давления с высотой — величина обратная вертикальному барическому градиенту и называемая барическая ступень, имеет размерность м/Па, показывающая на сколько метров нужно изменить высоту, чтобы давления изменилось на 1 Па.

Обычно горизонтальный барический градиент невелик и составляет 1—3 мбар на 100 км, но в тропических циклонах и ураганах иногда достигает десятков миллибар на 100 км.

В литературе можно встретить теперь нерекомендованные к использованию, разговорные термины «барометрический градиент» и «барометрическая ступень»[1].

Ненулевой горизонтальный барический градиент является одной из причин, которые приводят к возникновению ветра и циркуляции атмосферы.

Градиент | Математика | Fandom

Файл:Градиент холма.gif

Градиент (от , род. падеж gradientis — шагающий болт ) — характеристика, показывающая направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой. Например, если взять высоту поверхности Земли над уровнем моря (2-мерное пространство), то её градиент в каждой точке поверхности будет показывать «в горку».

Как видно из объяснения, градиент является векторной функцией, а величина, которую он характеризует — функцией скалярной.

Формально, для случая трёхмерного пространства, градиентом называется векторная функция с компонентами $ \frac {\partial \phi} {\partial x} $, $ \frac {\partial \phi} {\partial y} $, $ \frac {\partial \phi} {\partial z} $, где φ — некоторая скалярная функция координат x, y, z.

Если $ \phi $ — функция n переменных $ x_1,\ldots,x_n $, то её градиентом будет n-мерный вектор

$ \left(\frac{\partial \phi}{\partial x_1},\ldots,\frac{\partial \phi}{\partial x_n}\right) $,

компоненты которого равны частным производным $ \phi $ по всем её аргументам.

Градиент обозначается $ \mathrm{grad}\phi $ или, с использованием оператора набла, $ \nabla \phi $.

Из определения градиента следует, что:

$ \mathrm{grad}\phi = \nabla \phi = \frac {\partial \phi} {\partial x} \vec e_x + \frac {\partial \phi} {\partial y} \vec e_y + \frac {\partial \phi} {\partial z} \vec e_z $

    Свойства

    Для любого постоянного числа $ c\in\R $ и скалярных полей $ \vec{u}, \vec{v}:\R^n\to\R $ справедливо следующее:

    • $ \operatorname{grad}\,c=\vec{0} $

    Линейность

    • $ \operatorname{grad}\,(c\cdot \vec{u})=c\cdot\operatorname{grad}\,\vec{u} $
    • $ \operatorname{grad}\,(\vec{u}+\vec{v})=\operatorname{grad}\,\vec{u}+\operatorname{grad}\,\vec{v} $

    Правило Лейбница

    • $ \operatorname{grad}\,(\vec{u}\cdot \vec{v}) = \vec{u}\cdot\operatorname{grad}\,\vec{v} + \vec{v}\cdot\operatorname{grad}\,\vec{u} $, где $ \vec{u}\cdot\vec{v} $ — скалярное произведение векторов $ \vec u $ и $ \vec v $.

    Пример

    Например, градиент функции $ \phi(x,y,z)=2x+3y^2-sin(z) $ будет представлять собой:

    $ \nabla \phi = \begin{pmatrix} {\frac{\partial \phi}{\partial x}}, {\frac{\partial \phi}{\partial y}}, {\frac{\partial \phi}{\partial z}} \end{pmatrix} = \begin{pmatrix} {2,} { 6y,} { -cos(z)} \end{pmatrix} $

    В физике

    В различных отраслях физики используется понятие градиента различных физических полей.

    Например, градиент концентрации — нарастание или уменьшение по какому-либо направлению концентрации растворённого вещества, градиент температуры — увеличение или уменьшение по направлению температуры среды и т.д.. Градиент может быть вызван различными причинами, например, механическим препятствием, действием электромагнитных, гравитационных или других полей или различием в растворяющей способности граничащих фаз, например, октанол/вода.

    Связь с производной по направлению

    Используя правило дифференцирования сложной функции, нетрудно показать, что производная функции $ \phi $ по направлению $ \vec{e}=(e_1,\ldots,e_n) $ равняется скалярному произведению градиента $ \phi $ на единичный вектор $ \vec{e} $:

    $ \frac{\partial \phi}{\partial \vec e}=\frac{\partial \phi}{\partial x_1} e_1+\cdots+\frac{\partial \phi}{\partial x_n} e_n = (\nabla\!\phi,\vec e) $

    Таким образом, для вычисления производной по любому направлению достаточно знать градиент функции, то есть набор всех её частных производных.

    Градиент в ортогональных криволинейных координатах

    $ \operatorname{grad} U(q_1, q_2, q_3) = \frac{1}{H_1}\frac{\partial U}{\partial q_1}\vec i + \frac{1}{H_2}\frac{\partial U}{\partial q_2}\vec j + \frac{1}{H_3}\frac{\partial U}{\partial q_3}\vec k $,

    где Hi — коэффициенты Ламе.

    Цилиндрические координаты

    Коэффициенты Ламе:

    $ \begin{matrix}H_1 = 1 \\ H_2 = r \\ H_3 = 1 \end{matrix} $.

    Отсюда:

    $ \operatorname{grad} U(r, \theta, z) = \frac{\partial U}{\partial r}\vec r + \frac{1}{r}\frac{\partial U}{\partial \theta}\vec \theta + \frac{\partial U}{\partial z}\vec z $.

    Сферические координаты

    Коэффициенты Ламе:

    $ \begin{matrix}H_1 = 1 \\ H_2 = r \\ H_3 = r\sin{\theta} \end{matrix} $.

    Отсюда:

    $ \operatorname{grad} U(r, \theta, \phi) = \frac{\partial U}{\partial r}\vec r + \frac{1}{r}\frac{\partial U}{\partial \phi}\vec \phi + \frac{1}{r\sin{\theta}}\frac{\partial U}{\partial\theta }\vec \theta $.

    См. также

    cs:Gradienthe:גרדיאנטnl:Gradiënt pl:Gradient (matematyka)sl:Gradient sv:Gradient uk:Градієнт

    Градиент Википедия

    Операция градиента преобразует холм (слева), если смотреть на него сверху, в поле векторов (справа). Видно, что векторы направлены «в горку» и чем длиннее, тем круче наклон.

    Градие́нт (от лат. gradiens, род. п. gradientis «шагающий, растущий») — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины φ,{\displaystyle \varphi ,} значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.

    Например, если взять в качестве φ{\displaystyle \varphi } высоту поверхности земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.

    Другими словами, градиент — это производная по пространству, но в отличие от производной по одномерному времени, градиент является не скаляром, а векторной величиной.

    С математической точки зрения на градиент можно смотреть как на:

    1. Коэффициент линейности изменения значения функции многих переменных от изменения значения аргумента;
    2. Вектор в пространстве области определения скалярной функции многих переменных, составленный из частных производных;
    3. Строки матрицы Якоби содержат градиенты составных скалярных функций из которых состоит векторная функция многих переменных.

    Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности любой физической природы или чисто абстрактным (безразмерным).

    Термин впервые появился в метеорологии, а в математику был введён Максвеллом в 1873 г.; обозначение grad{\displaystyle \mathrm {grad} } тоже предложил Максвелл.

    Стандартные обозначения:

    gradφ{\displaystyle \mathrm {grad} \,\varphi }

    или, с использованием оператора набла,

    ∇φ{\displaystyle \nabla \varphi }

    — вместо φ{\displaystyle \varphi } может быть любое скалярное поле, обозначенное любой буквой, например gradV,∇V{\displaystyle \mathrm {grad} \,V,\nabla V} — обозначения градиента поля: V{\displaystyle V}.

    Гистограмма направленных градиентов — Википедия

    Эта статья или раздел содержит незавершённый перевод с английского языка.

    Вы можете помочь проекту, закончив перевод.

    Гистограмма направленных градиентов (англ. Histogram of Oriented Gradients, HOG) — дескрипторы особых точек, которые используются в компьютерном зрении и обработке изображений с целью распознавания объектов. Данная техника основана на подсчете количества направлений градиента в локальных областях изображения. Этот метод похож на гистограммы направления края, дескрипторы SIFT и контексты формы, но отличается тем, что вычисляется на плотной сетке равномерно распределенных ячеек и использует нормализацию перекрывающегося локального контраста для увеличения точности.

    Навнит Далал и Билл Триггс, исследователи INRIA, впервые описали гистограмму направленных градиентов в своей работе на CVPR в июне 2005 года. В этой работе они использовали алгоритм для нахождения пешеходов на статичных изображениях, хотя впоследствии расширили область применения до нахождения людей на видео, а также различных животных и машин на статичных изображениях.

    Основной идеей алгоритма является допущение, что внешний вид и форма объекта на участке изображения могут быть описаны распределением градиентов интенсивности или направлением краев. Реализация этих дескрипторов может быть произведена путём разделения изображения на маленькие связные области, именуемые ячейками, и расчетом для каждой ячейки гистограммы направлений градиентов или направлений краев для пикселей, находящихся внутри ячейки. Комбинация этих гистограмм и является дескриптором. Для увеличения точности локальные гистограммы подвергаются нормализации по контрасту. С этой целью вычисляется мера интенсивности на большем фрагменте изображения, который называется блоком, и полученное значение используется для нормализации. Нормализованные дескрипторы обладают лучшей инвариантностью по отношению к освещению.

    Дескриптор HOG имеет несколько преимуществ над другими дескрипторами. Поскольку HOG работает локально, метод поддерживает инвариантность геометрических и фотометрических преобразований, за исключением ориентации объекта. Подобные изменения появятся только в больших фрагментах изображения. Более того, как обнаружили Далал и Триггс, грубое разбиение пространства, точное вычисление направлений и сильная локальная фотометрическая нормализация позволяют игнорировать движения пешеходов, если они поддерживают вертикальное положение тела. Дескриптор HOG, таким образом, является хорошим средством нахождения людей на изображениях.

    [1]

    Вычисление градиента[править | править код]

    Первым шагом вычислений во многих детекторах особых точек является нормализация цвета и гамма-коррекция. Далал и Триггс установили, что для дескриптора HOG этот шаг можно опустить, поскольку последующая нормализация даст тот же результат. Поэтому на первом шаге рассчитываются значения градиентов. Самым распространенным методом является применение одномерной дифференцирующей маски в горизонтальном и/или вертикальном направлении. Этот метод требует фильтрации цветовой или яркостной составляющей при помощи следующих фильтрующих ядер:

    [−1,0,1]{\displaystyle [-1,0,1]} и [−1,0,1]T.{\displaystyle [-1,0,1]^{T}.}

    Далал и Триггс использовали более сложные маски, такие как Собел 3×3 (Оператор Собеля) или диагональные маски, но эти маски показали более низкую производительность для данной задачи. Они также экспериментировали с размытием по Гауссу перед применением дифференцирующей маски, но также обнаружили, что пропуск этого шага увеличивает быстродействие без заметной потери качества.[2]

    Группировка направлений[править | править код]

    На следующем шаге вычисляются гистограммы ячеек. Каждый пиксел в ячейке участвует во взвешенном голосовании для каналов гистограммы направлений, основанном на значении градиентов. Ячейки могут быть прямоугольной или круглой формы, каналы гистограммы равномерно распределяются от 0 до 180 или же от 0 до 360 градусов, в зависимости от того, вычисляется «знаковый» или «беззнаковый градиент». Далал и Триггс обнаружили, что беззнаковый градиент совместно с девятью каналами гистограммы дает лучшие результаты при распознавании людей. При распределении весов в голосовании вес пикселя может задаваться либо абсолютным значением градиента, либо некоторой функцией от него; в реальных тестах абсолютное значение градиента дает лучшие результаты. Другими возможными вариантами могут быть квадратный корень, квадрат или урезанное абсолютное значение градиента.[3]

    Блоки дескрипторов[править | править код]

    Для принятия во внимание яркости и контрастности градиенты следует локально нормировать, для чего ячейки нужно сгруппировать в более крупные связные блоки. Дескриптор HOG, таким образом, является вектором компонент нормированных гистограмм ячеек из всех областей блока. Как правило, блоки перекрываются, то есть каждая ячейка входит более чем в один конечный дескриптор. Используются две основные геометрии блока: прямоугольные R-HOG и круглые C-HOG. Блоки R-HOG обычно являются квадратными сетками, характеризующимися тремя параметрами: количеством ячеек на блок, количеством пикселов на ячейку и количеством каналов на гистограмму ячейки. В эксперименте Далала и Триггса оптимальными параметрами являются блоки 16×16, ячейки 8×8 и 9 каналов на гистограмму. Более того, они обнаружили, что можно слегка повысить скорость вычислений, применяя гауссов фильтр внутри каждого блока до процедуры голосования, что, в свою очередь, снижает вес пикселей на границах блоков. Блоки R-HOG оказываются очень похожими на SIFT-дескрипторы; однако, несмотря на их похожую структуру, блоки R-HOG вычисляются на плотных сетках фиксированного масштаба без фиксированного направления, в то время как SIFT-дескрипторы вычисляются в разреженных, не чувствительных к масштабу ключевых точках изображения и используют поворот для выравнивания направления. Кроме того, для кодирования информации о форме объектов блоки R-HOG используются совместно, в то время как SIFT-дескрипторы используются по отдельности.

    Блоки C-HOG имеют 2 разновидности: с цельной центральной ячейкой и разделенной на сектора. Эти блоки могут быть описаны 4 параметрами: количество секторов и колец, радиус центрального кольца и коэффициент расширения для радиусов остальных колец. Далал и Триггс обнаружили, что обе разновидности показали одинаковый результат, и разделение на 2 кольца и 4 сектора с радиусом 4 пиксела и коэффициентом расширения 2 дало лучший результат в их эксперименте. Кроме того, гауссово взвешивание не дало никаких улучшений при использовании блоков C-HOG. Эти блоки похожи на контексты формы, но имеют важное отличие: блоки C-HOG содержат ячейки с несколькими каналами направлений, в то время как контексты формы используют только наличие одного края.[4]

    Нормализация блоков[править | править код]

    Далал и Триггс исследовали четыре метода нормализации блоков. Пусть v{\displaystyle v} — ненормированный вектор, содержащий все гистограммы данного блока, ‖v‖k{\displaystyle \|v\|_{k}} — его k-норма при k=1,2{\displaystyle k={1,2}} и e{\displaystyle e} — некая малая константа (точное значение не так важно). Тогда нормировочный множитель можно получить одним из следующих способов:

    L2-норма: f=v‖v‖22+e2{\displaystyle f={v \over {\sqrt {\|v\|_{2}^{2}+e^{2}}}}}
    L2-hys: L2-норма ограничивается сверху (значения v, бóльшие 0,2, полагаются равными 0,2) и перенормируется, как в[5]
    L1-норма: f=v(‖v‖1+e){\displaystyle f={v \over (\|v\|_{1}+e)}}
    корень из L1-нормы: f=v(‖v‖1+e){\displaystyle f={\sqrt {v \over (\|v\|_{1}+e)}}}

    Далал и Триггс установили, что L1-норма дает менее надежные результаты, чем остальные три, которые работают приблизительно одинаково хорошо, однако все четыре метода значительно улучшают результаты по сравнению с ненормализованными.[4]

    SVM-классификатор[править | править код]

    Конечным шагом в распознавании объектов с использованием HOG является классификация дескрипторов при помощи системы обучения с учителем. Далал и Триггс использовали метод опорных векторов (SVM, Support Vector Machine).

    В оригинальном эксперименте по обнаружению людей, Далал и Триггс сравнивали дескрипторы R-HOG и C-HOG с обобщенными вейвлетами Хаара и контекстами формы. Обобщенные вейвлеты Хаара являются направленными вейвлетами Хаара и были использованы в 2001 году Моханом, Папагеоргиу и Поггио в их экспериментах по обнаружению объектов. Дескрипторы PCA-SIFT похожи на SIFT-дескрипторы, но отличаются тем, что к нормализованным градиентам применяется метод главных компонент. Дескрипторы PCA-SIFT впервые были использованы в 2004 в работе Ке и Суктханкара; было заявлено, что они по своим параметрам превосходят обычные SIFT-дескрипторы. Наконец, контексты формы, подобно C-HOG, используют круглые бины, но учитывают голоса только на основе присутствия края, не учитывая ориентацию. Контексты формы появились в 2001 в работе Белонги, Малик и Пузича.

    Тестирование проводилось на двух разных наборах данных. База данных пешеходов Массачусетского технологического института содержит обучающую выборку из 509 изображений и тестовую выборку из 200 изображений. Набор содержит изображения людей только спереди или сзади, позы на изображениях почти не отличаются. Эта база данных широко известна и используется в других исследованиях, найти её можно по ссылке https://web.archive.org/web/20080130190339/http://cbcl.mit.edu/cbcl/software-datasets/PedestrianData.html. Второй набор данных был специально создан Далалом и Триггсом для их эксперимента, поскольку на наборе MIT дескрипторы HOG показали почти совершенные результаты. Этот набор данных, известный как INRIA, содержит 1805 изображений людей. Набор содержит изображения людей в широком разнообразии поз, включает в себя изображения с трудным фоном (например, на фоне толпы), и является гораздо более сложным для распознавания, чем набор MIT. База данных INRIA в настоящий момент доступна по адресу http://lear.inrialpes.fr/data.

    По результатам исследований, дескрипторы C-HOG и R-HOG дают сравнимые результаты, причем C-HOG имеют несколько меньшую долю пропущенных изображений при фиксированной доле ошибок первого рода на обоих наборах изображений.

    ДескрипторНабор изображенийДоля пропущенных изображенийДоля ошибок первого рода
    HOGMIT≈010−4
    HOGINRIA0.110−4
    Обобщенные вейвлеты ХаараMIT0.0110−4
    Обобщенные вейвлеты ХаараINRIA0.310−4
    PCA-SIFT, контексты формыMIT0.110−4
    PCA-SIFT, контексты формыINRIA0.510−4

    По следующей ссылке можно найти соответствующий график DET.[2]

    В рамках семинара Pascal Visual Object Classes в 2006 году, Далал и Триггс представили результаты применения HOG-дескрипторов к поиску на изображениях не только людей, но и машин, автобусов, велосипедов, собак, кошек и коров, а также оптимальные параметры для формирования и нормализации блоков в каждом случае. По ссылке можно посмотреть примеры для обнаружения мотоциклов.[6]

    Затем в рамках Европейской конференции по компьютерному зрению 2006 года, Далал и Триггс совместно с Корделией Шмид применили HOG-дескрипторы к распознаванию людей на видео. Предложенный ими способ заключается в совместном использовании обычных HOG-дескрипторов на каждом кадре и гистограмм внутреннего движения (англ. Internal Motion Histograms, IMH) на парах последовательных кадров. IMH-дескрипторы используют длины градиентов, полученных из оптического потока между двумя последовательными кадрами.

    Шаблон:Градиент — Википедия

    Этот шаблон создает градиент фона. В настоящее время работает в Firefox (3,6 и выше), Opera (11.10 и выше), Safari (4,0 и выше) и Google Chrome.
    Internet Explorer его не поддерживает.

    Использование

    {{gradient|#начальный цвет|#конечный цвет|направление}}

    или

    {{градиент|#начальный цвет|#конечный цвет|направление}}
    • Начальный цвет (обязательно) — Начальный цвет градиента.
    • Конечный цвет (обязательно) — Конечный цвет градиента.
    • Направление (необязательно) — (horizontal) или вертикальная (vertical).

    Примеры

    <div>Lorem ipsum...*...est laborum.</div>

    Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.

    <div>Lorem ipsum...*...est laborum.</div>

    Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.

    <div>Lorem ipsum...*...est laborum.</div>

    Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.

    Примечание: В приведенных выше примерах используются контрастные цвета, чтобы показать эффект более четко. Но на деле лучше использовать цвета с небольшими различиями, чтобы улучшить внешний вид, а не радикально изменить его. Это также сводит к минимуму различия между страницами, открытыми в разных браузерах.

    См. также

Categories: Разное

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *