Гипотеза Тёплица — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 ноября 2016; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 ноября 2016; проверки требует 1 правка.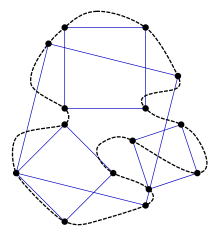 Пунктирная кривая проходит через вершины нескольких квадратов

Гипотеза Тёплица, также известная как гипотеза о вписанном квадрате — нерешённая проблема геометрии. Формулировка гипотезы:

На всякой простой замкнутой плоской жордановой кривой можно отыскать четыре точки, лежащие в вершинах квадрата.

Гипотеза Тёплица верна для выпуклых кривых, кусочно-гладких кривых и в других специальных случаях. Проблема была сформулирована Отто Тёплицем в 1911 году

[1]. Ранние положительные результаты были получены Арнольдом Эмчем^[2] и Львом Шнирельманом^[3]. По состоянию на 2016 г. гипотеза в общем случае остаётся не доказанной.

Пусть C — кривая Жордана. Многоугольник P вписан в C , если все вершины P принадлежат C. Проблема вписанного квадрата заключается в следующем:

Можно ли на каждой кривой Жордана отыскать вписанный квадрат?

При этом не требуется, чтобы вершины квадрата находились в каком-либо определённом порядке.

Для некоторых кривых, например, для окружности и квадрата, можно указать бесконечно много вписанных квадратов. В тупоугольный треугольник можно вписать ровно один квадрат.

Вальтер Стромквист доказал, что в каждую локально монотонную простую плоскую кривую можно вписать квадрат^[4]. Доказательство применимо к кривым C, обладающим свойством локальной монотонности: для любой точки

p, лежащей на C, существует такая окрестность U(p), что ни одна хорда C в этой окрестности не является параллельной заданному направлению n(p) (направлению оси ординат). К локально монотонным кривым относятся все выпуклые кривые и все кусочно-заданные непрерывно дифференцируемые кривые без точек возврата.

Утвердительный ответ также известен для центрально симметричных кривых^[5].

Известно, что для любого заданного треугольника T и жордановой кривой C существует треугольник, подобный T и вписанный в C^[6][7]. Более того, множество вершин таких треугольников является плотным в C^[8]. В частности, всегда существует вписанный равносторонний треугольник. Также в любую жорданову кривую можно вписать прямоугольник.

В некоторых обобщениях проблемы вписанного квадрата рассматриваются вписанные в кривые многоугольники. Существуют также обобщения для многомерных евклидовых пространств. Так, Стромквист доказал, что в любую непрерывную замкнутую кривую C∈Rn{\displaystyle C\in R^{n}}, удовлетворяющую «условию A», можно вписать четырёхугольник с равными сторонами и равными диагоналями; «условие A» заключается в том, что никакие две хорды

C в соответствующей окрестности любой точки не должны быть перпендикулярными^[4]. Этот класс кривых включает все кривые C². Нильсен и Райт доказали, что любой симметричный континуум K∈Rn{\displaystyle K\in R^{n}} содержит вписанные прямоугольники^[5]. Генрих Гуггенхаймер доказал, что любая гиперповерхность, C³-диффеоморфная сфере Sⁿ⁻¹, содержит 2ⁿ вершин правильного евклидова гиперкуба^[9].

1. ↑ Toeplitz, O. : Ueber einige aufgaben der analysis situs Verhandlungen der Schweizerischen Naturforschenden Gesellschaft in Solothurn, 94 (1911), p. 197.
2. ↑ Emch, Arnold (1916), «On some properties of the medians of closed continuous curves formed by analytic arcs», American Journal of Mathematics Т. 38 (1): 6–18, DOI 10.2307/2370541 
3. ↑ Лев Шнирельман. О некоторых геометрических свойствах замкнутых кривых // УМН. — 1944. — Т. 10. — С. 34—44.
4. ↑ ^{1 2} Stromquist, Walter (1989), «Inscribed squares and square-like quadrilaterals in closed curves», Mathematika Т. 36 (2): 187–197, DOI 10.1112/S0025579300013061 
5. ↑ ^{1 2} Nielsen, Mark J. & Wright, S. E. (1995), «Rectangles inscribed in symmetric continua», Geometriae Dedicata Т. 56 (3): 285–297, DOI 10.1007/BF01263570 
6. ↑ Meyerson, Mark D. (1980), «Equilateral triangles and continuous curves», Fundamenta Mathematicae Т. 110 (1): 1–9 .
7. ↑ Kronheimer, E. H. & Kronheimer, P. B. (1981), «The tripos problem», Journal of the London Mathematical Society, Second Series Т. 24 (1): 182–192, DOI 10.1112/jlms/s2-24.1.182 
8. ↑ Nielsen, Mark J. (1992), «Triangles inscribed in simple closed curves», Geometriae Dedicata Т. 43 (3): 291–297, DOI 10.1007/BF00151519 
9. ↑ Guggenheimer, H. (1965), «Finite sets on curves and surfaces», Israel Journal of Mathematics Т. 3: 104–112, DOI 10.1007/BF02760036 

Квадрирование квадрата — Википедия

Материал из Википедии — свободной энциклопедии

Разбиение квадрата на 21 квадрат, среди которых нет равных. Число внутри каждого квадрата означает длину его стороны. Соответственно, длина стороны большого квадрата равна (складывая длины сторон крайних квадратов) 50 + 35 + 27 = 50 + 29 + 33 = 33 + 37 + 42 = 27 + 19 + 24 + 42 = 112

Квадри́рование квадра́та — задача о разбиении квадрата на конечное число меньших квадратов. В более узком смысле — задача о разбиении квадрата на конечное число попарно неравных между собой квадратов.

В 1936—1938 годах её решили четверо студентов Тринити-колледжа Кембриджского университета^[1].

• Квадрат, разбитый на попарно неравные квадраты, называется совершенным.
• Порядком квадрата, разбитого на составные квадраты, называется число составляющих его квадратов.
• Разбиение квадрата, никакое подмножество квадратов которого не образует прямоугольник (не считая отдельных квадратов), называется простым.

• Вопрос о возможности разбиения квадрата на неравные квадраты был записан в Шотландской книге Станиславом Рузевичем под номером 59^[2] в 1935-м году.
• Самые первые найденные Бруксом, Смитом, Стоуном и Таттом совершенные квадраты были 69-го порядка.
• В 1939 году Р. Шпраг (R. Sprague) нашёл совершенный квадрат 55-го порядка, это было первое опубликованное решение для совершенного квадрата.
• Позднее Т. Г. Уиллкокс (T. H. Willcocks) нашёл совершенный квадрат 24-го порядка, который долгое время держал рекорд малости порядка.
• В 1978 году голландский математик А. Й. В. Дёйвестейн (A. J. W. Duijvestijn) с помощью компьютера нашёл разбиение квадрата на 21 квадрат, среди которых нет равных (см. рис.). Он также доказал следующие утверждения:
  • Не существует совершенного квадрата меньшего порядка.
  • Найденное им разбиение — единственно возможное для разбиения 21-го порядка.

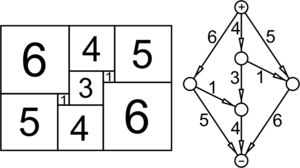Диаграмма Смита для прямоугольника. Верхняя клемма «+» соответствует верхней стороне прямоугольника, нижняя клемма «−» — нижней стороне. Остальные клеммы соответствуют промежуточным горизонтальным отрезкам. Если длине стороны квадрата сопоставить силу тока, то диаграмма становится электрической схемой, для которой выполняются правила Кирхгофа. Например, длина верхней стороны прямоугольника складывается из сторон 6 + 4 + 5 = 15, что соответствует разветвлению тока в 15 единиц на три пропорциональные части.

Ключевую роль в решении задачи квадрирования сыграло предложение для анализа диаграммы, названной диаграммой Смита, которая любому разбиению квадрата (или прямоугольника) ставит в соответствие электрическую цепь. Это позволило применять для решения задачи квадрирования хорошо разработанную теорию электрических цепей.

Можно считать, что прямоугольник это проводник сделанный из фольги с постоянным удельным сопротивлением. Если вдоль оснований подлючён ток, то сопротивление прямоугольника прямопропоционально высоте и обратно пропорционально ширине прямоугольника. Поэтому можно считать что сопротивление любого квадрата единица.

Каждому горизонтальному отрезку на схеме разбиения квадрата соответствует «клемма» этой цепи, а каждому квадрату разбиения — проводник, соединяющий две «клеммы». Сила тока, текущего по проводнику, равна длине стороны соответствующего квадрата. Поскольку можно считать, что сопротивление каждого квадрата равно единице, такая электрическая цепь ведёт себя как «настоящая»; в частности, подчиняется правилам Кирхгофа для токов в цепи.

Число простых совершенных квадрированных квадратов порядка n с точностью до^[en] симметрий указано в последовательности A006983 в OEIS^[3]. В 2013 году было найдено число квадратов порядка 32 (144 161)^[3][4]. В июне 2014 года Джим Уильямс (Jim Williams) получил все 378 197 простых совершенных квадрированных квадратов порядка 33

[4].

n	Число простых совершенных квадратов порядка n
21	1
22	8
23	12
24	26
25	160
26	441
27	1152
28	3001
29	7901
30	20 566
31	54 541
32	144 161
33	378 197[4]

«Кубирование куба», то есть разбиение куба на конечное число попарно неравных между собой кубов, невозможно. Доказательство этого факта было дано Бруксом, Смитом, Стоуном и Таттом.

Доказательство

Допустим, что искомое разбиение куба существует.

Рассмотрим одну из граней куба, очевидно, не уменьшая общность, можно выбрать нижнюю грань.

На нижней грани стоят разновеликие кубы, своими нижними рёбрами разбивающие грань на разновеликие квадраты.

Найдём самый маленький квадрат разбиения нижней грани. Очевидно, что этот квадрат не может примыкать к ребру куба, будучи ограничен сторонами бо́льших квадратов, следовательно, он должен располагаться где-то внутри грани.

Теперь рассмотрим верхнюю грань этого малого кубика. Поскольку по предположению это самый маленький кубик на нижней грани куба, он окружен более высокими кубами. Поэтому на его верхнюю грань не заступает ни один соседний куб. Следовательно, стоящие на этой грани кубики меньшего размера снова разбивают верхнюю грань этого кубика на разновеликие квадраты, причём самый малый квадрат разбиения верхней грани рассматриваемого кубика снова не может принадлежать ребру кубика и находится внутри грани.

Продолжая этот процесс рассуждения, приходим к противоречию, что доказывает теорему.

Также легко доказывается теорема о невозможности «гиперкубирования гиперкуба» для гиперкубов любой размерности, большей 3-х. Действительно, для любой размерности

n гиперкубы разбиения, прилегающие к какой-либо (n − 1)-мерной гиперграни исходного гиперкуба, должны разбивать эту гипергрань на конечное число попарно неравных (n − 1)-мерных гиперкубов. При n = 4 «гиперкубирование» невозможно, так как должно порождать «кубирование» 3-мерных гиперграней исходного 4-мерного гиперкуба. Индукцией по n можно сделать заключение о невозможности «гиперкубирования» для всех n > 3.

• Гарднер М., Математические головоломки и развлечения. Пер. с английского Ю. Данилова. Изд. «Оникс», Москва, 1994, стр. 305—326.
• Яглом И. М. Как разрезать квадрат серия «Математическая библиотечка» М., Наука, 1968—112 с.
• Bouwkamp C. J., Duijvestijn A. J. W. Catalogue of Simple Perfect Squared Squares of Orders 21 Through 25, Eindhoven Univ. Technology, Dept. of Math., Report 92-WSK-03, Nov. 1992.
• Bouwkamp C. J., Duijvestijn A. J. W. Album of Simple Perfect Squared Squares of order 26, Eindhoven University of Technology, Faculty of Mathematics and Computing Science, EUT Report 94-WSK-02, December 1994.
• Brooks, R. L., Smith C. A. B., Stone, A. H., Tutte, W. T. The Dissection of Rectangles into Squares, Duke Math. J. 7, 312—340, 1940
• Gardner Martin, Squaring the square, in The 2nd Scientific American Book of Mathematical Puzzles and Diversions.
• Meschkowski H. Unsolved and Unsolvable Problems in Geometry, Oliver and Boyd, 1966, Edinburgh, pp. 9—102.
• Stein S. Mathematics: The Man-Made Universe, (2nd ed.) Freeman and Co., 1969, San Francisco, pp. 92—124.
• Tutte W. Squaring the Square, Canadian journal of Mathematics, 1950, pp.197—209.
• Tutte W. The Quest of the Perfect Square,
  The American Mathematical Monthly, 1965, Vol. 72, No. 2, pp. 29—35.

Квадрат. Свойства квадрат. Признаки квадрата.

Категория: Справочные материалы

Елена Репина 2013-07-26 2013-09-20

Квадрат – ромб, у которого все углы прямые.

или

Квадрат – прямоугольник с равными сторонами.

или

Квадрат – параллелограмм, у которого все стороны равны  и все углы равны.

Свойства квадрата

 

 

Все свойства параллелограмма, ромба, прямоугольника верны  для квадрата.

 

Признаки квадрата

 

Четырехугольник будет являться квадратом, если выполняется хотя бы одно из условий:

1. Все стороны равны и среди внутренних углов есть прямой угол.

2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

3. Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90˚.

Описанная окружность

 

Около квадрата можно описать окружность. Сторона и радиус окружности связаны соотношением:

Вписанная окружность

 

В квадрат можно вписать окружность. Радиус вписанной окружности и сторона квадрата связаны соотношением:

Площадь квадрата

 

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Автор: egeMax | Нет комментариев

Гардероб для фигуры «Квадрат» | Мода от Кутюр.Ru

 Телосложение – это то, что дано нам природой. А с природой, как известно, бороться бесполезно. Если у женщины, как говориться, широкая кость, то никакие спортивные занятия и диеты не превратят ее в тоненькую «фею». Но если научиться правильно подбирать одежду, привлекательно выглядеть можно, независимо от типа фигуры.

 

Особенности фигуры

 

 Женщины, имеющие фигуру типа «квадрат», не отличаются изяществом форм. Объемы талии, бедер и груди у них практически одинаковы. Но, в отличие от фигуры типа «прямоугольник», которая тоже не имеет приятных изгибов, женщины-«квадраты» еще и довольно крупные.

 Именно про такое телосложение принято говорить «широкая» кость. Кроме того, у «квадратов» при наборе лишнего веса появляется выраженный животик. А вот ноги могут оставаться достаточно стройными, особенно в области от колен до щиколоток.

Основные черты телосложения:

• коренастое тело;
• широкая грудная клетка;
• полное отсутствие талии;
• широкий таз и плоские ягодицы;
• небольшой рост;
• пышный бюст.

 

Рекомендации по похудению

 

 К сожалению, никакие диеты не приведут к тому, что дама с телосложением типа «квадрат» сможет приобрести модельные параметры. Даже при отсутствии лишнего веса такие фигуры кажутся массивными.

 Предрасположенность к полноте у обладательниц фигуры в форме квадрата высокая. При наборе лишних килограммов фигура становится еще более массивной, появляется выраженный живот. Поэтому нужно стараться держать себя в форме.

 

Особенности подбора гардероба

 

 Чтобы выглядеть более изящной, нужно научиться правильно подбирать гардероб и использовать плюсы своей фигуры. Такими плюсами являются:

• Ноги. Даже у полных женщин ноги зачастую остаются стройными.

 

• Грудь. У обладательниц такого телосложения бюст, как правило, пышный.​

Основная задача при подборе нарядов заключается в том, чтобы сделать образ более женственным и создать видимость наличия талии.

 

Стилисты рекомендуют выбирать:

• одежду прямых фасонов, она не акцентирует внимания на линии талии;

 

• платья и блузки в стиле ампир, эти модели позволят продемонстрировать грудь и скроют выступающий животик;

 

• одежду из тканей, которые хорошо держат форму, она хорошо скрадывает особенности фигуры;

 

• рекомендуется использовать асимметричный крой и асимметричные детали, чтобы скрыть отсутствие талии;

 

• чтобы подчеркнуть грудь, стоит выбирать одежду с глубоким овальным или V образным декольте;

 

• визуально придать фигуре изгибы можно, используя юбки покроя полусолнце. Но при выборе этого фасона нужно не перестараться, слишком пышная юбка на коренастой фигуре будет выглядеть нелепо;

 

• обязательно нужно использовать ткани в полоску. Горизонтально расположенная полоска на лифе и диагональные линии в области талии сделают силуэт более женственным. Хорошо смотрятся с двухцветные модели с темными боковыми вставками на боках.

 

 Обладательницам фигуры «квадрат» следует отказаться от следующих видов одежды:

• юбки на резинке или присборенные в области талии;
• брюки, юбки, джинсы с низкой посадкой в сочетании с укороченным топом;
• обтягивающие вещи;
• одежда «балахонистого» типа, она превратит вашу фигуру в «копну».

 

Рекомендации по выбору одежды

 

 Чтобы выглядеть более привлекательно, необходимо правильно подбирать фасоны одежды и умело использовать цветовые сочетания.

 

Платья

• Идеальным фасоном является платье в стиле ампир. Единственное ограничение – нужно избегать пышных рукавов-фонариков. Лиф платья позволит подчеркнуть красивую грудь, а ниспадающая прямо от линии груди юбка скроет все недостатки телосложения.

 

• Можно шить платья прямого силуэта. Чтобы выглядеть в таком наряде привлекательнее, стоит использовать ткани в полоску. Хорошо смотрятся и модели, в которых по бокам в области талии имеются вставки более темного оттенка.

• Платья с запахом и асимметричными деталями помогу придать фигуре более женственные очертания. Также хорошо смотрятся модели с декоративными швами, расположенными асимметрично.

• Если вес в норме, то девушки могут позволить себе платья с лифом полуприлегающего силуэта и расклешенной юбкой. Можно сшить и платье-футляр прямого силуэта из ткани, которая хорошо держит форму.

Длину платья лучше выбирать минимум до колена. Даже если ноги стройные, то короткие платья на фигуре «квадрат» смотрятся некрасиво.

 Для вечернего платья стоит выбрать шелк, шифон или другую струящуюся ткань. Туалет можно сделать с асимметричным вырезом или с глубоким декольте и завышенной линией талии. 

 

Юбки

 При выборе юбки нужно помнить об умеренности. Модель не должна быть слишком узкой, и слишком пышной, не стоит шить юбку из ткани с узором или крупной клеткой. Нужно найти золотую середину. Лучшие фасоны юбок – трапециевидные или годе. При отсутствии лишнего веса можно шить модели покроя полусолнце.

Плохо смотрятся на фигурах, напоминающих по форме квадрат, узкие и зауженные к низу юбки.

 Для того чтобы визуально вытянуть силуэт, используют декоративные детали – вертикальные канты, отстрочки, разрезы.

 

Брюки

 Брюки – вещь практичная и всесезонная. Дамам с фигурой квадрат нет необходимости отказываться от этого предмета гардероба. Для лета нужно выбирать брюки из льна, плотного шелка или хлопковых смесовых тканей. Материя должна струиться, а не образовывать некрасивые складки. Для холодного сезона используют костюмные ткани, которые хорошо держат форму, плотный трикотаж.

Категорически противопоказаны фактурные ткани и букле, так как они добавляют объема.

 Лучший фасон – классический прямой покрой. Брюки не должны обтягивать, но и слишком широкие модели не подходят. Можно использовать расклешенные брюки, только клеш должен быть умеренным.

 

Блузы и жакеты

 Для квадратной фигуры хорошо подходят туники из легких струящихся тканей. Вырез лучше делать глубоким в виде букв V или U. Длина – до середины бедра.

 Можно поэкспериментировать, надев поверх светлой блузы темный корсет. При помощи этой детали туалета можно будет попытаться сформировать талию, а грудь и бедра предстанут во всей красе. Но при наличии заметно выступающего живота от корсетов придется отказаться.

 Майки и топы выбирайте полуприлегающие и удлиненные. А вот от моделей на тонких бретельках стоит отказаться, они будут нелепо смотреться на фоне широкой грудной клетки.

 Жакеты носите прямого силуэта. Длина – до середины бедер. Укороченные жакеты только подчеркнут отсутствие талии.

 

Верхняя одежда

 При покупке шубы стоит отдать предпочтение моделям из гладкого стриженого меха. Лучший крой – пиджачный, длина – до середины бедра, без капюшонов и других декоративных деталей. Если выбрана приталенная модель, то вместо мехового пояса используйте гладкий кожаный ремень, это избавит от дополнительного объема в области талии.

 Пальто лучше приобрести классическое, двубортное, носят его с широким кожаным поясом. Длину пальто можно варьировать от линии середины бедер до щиколотки. Но последний вариант подойдет, если рост не мене 170 см.

Хорошо подходит к фигуре «квадрат» пальто с кокеткой или с завышенной линией тали и трапециевидным низом. Такая модель подойдет и для невысоких девушек.

 При выборе курток стоит избегать укороченных моделей, а также, стеганных полосами или квадратами. Лучше предпочесть удлиненные куртки с гладкой поверхностью и асимметричными деталями. Например, линия застежки может проходить не по середины переда, а быть смещена в сторону.

 

Купальники

 Главное правило при подборе пляжного наряда – это умелое комбинирование. Скрыть выступающий живот помогут диагональные и вертикальные полосы на купальном костюме, а чтобы продемонстрировать красивую грудь, выбирайте лиф с V-образным вырезом.

 Для фигуры типа квадрат можно выбрать купальный костюм танкини. Его верх представлен в виде маечки, благодаря которой можно скрыть живот и отсутствие талии. Верх купальника должен иметь широкие лямки и узор, визуально формирующий талию. Хорошо подходят и модели с бретелью-петлей, этот фасон визуально сужает плечи.

Самый лучший вариант цветового решения для купального костюма обладательницы фигуры «квадрат» – это светлый верх, темная широкая полоса на талии и светлый низ.

 

Аксессуары

Обувь следует выбирать женственную и элегантную. Спортивный стиль не подходит. Можно носить и балетки, и туфли на шпильке. Но лучший вариант – обувь на устойчивом каблуке.

Сумки, желательно приобретать прямоугольной формы. Это позволит избежать нежелательного контраста между округлыми линиями аксессуаров и угловатой фигурой. 

Украшения подойдут неброские, массивные колье и подвески будут выглядеть слишком громоздко. Смело можно выбирать украшения с графическим дизайном, длинные бусы, заметные броши. Ремни лучше покупать широкие, но имеющие гладкую фактуру и без дополнительного декора. 

Шейные платки и шарфы обязательно должны быть в гардеробе, особенно хорошо смотрятся длинные шарфики и платки, повязанные вокруг шеи.

 

Модные образы

 

 Приведем несколько рекомендаций стилистов для создания модного образа для девушки с фигурой «квадрат»

 

Летний образ

 Летнее платье полуприлегаюшего силуэта бирюзового цвета украшено контрастными вертикальными кантами от линии плеча до низа. Дополним образ лакированным прямоугольным клатчем, открытыми туфлями кремового оттенка на каблуке. Если вечер выдался прохладным, наденем к платью удлиненный кардиган прямого силуэта молочно-белого цвета.

 

Весенний образ

 Прямые брюки цвета молочного шоколада создадут модный образ в комплекте с кремовой блузой полуприталенного фасона и втачными узкими рукавами. Дополним комплект плащом прямого кроя до середины бедра песочного оттенка, удобными лоферами леопардовой расцветки и дамской сумкой с короткой ручкой.

 

Осенний образ

 Пальто фиалкового оттенка на кокетке имеет небольшой отложной воротничок и рукава три четверти. Дополним его желто-розовым шейным платком, стальными черными перчатками до локтя и классическими ботильонами.

 

Известные личности с таким типом фигуры

 

 Среди известных личностей встречаются обладательницы фигуры типа квадрат. Благодаря удачно подобранным нарядам и правильно выбранным позам, зрители и не догадываются, что у многих звезд кино практически нет талии.

 Так, Мисси Перегрим является обладательницей широких мужских плеч и отличается полным отсутствием талии. Американская певица, известная, как Кеша, имеет фигуру, контуры которой явно напоминают квадрат.

Так что, не стоит расстраиваться, если фигура не имеет женственных изгибов, правильно подбирайте гардероб и будьте красивыми.

 

 

 

 

Facebook

Twitter

Вконтакте

Google+

Магический квадрат Дюрера — Блог доброй ведьмы

Есть некая гравюра «Меланхолия», принадлежащая немецкому художнику Альбрехту Дюреру, которая больше известна математикам и оккультистам, чем интересующимся живописью.

По крайней мере — вы можете это проверить — на просторах интернета о ней написано крайне мало. А ведь это реально крутая вещь. И единственным более-менее подробным источником является книга Дэна Брауна «Утраченный символ».

Я эту книгу прочитала и в голове не отложился ни сюжет, ни квадрат. И вот случайно вспыло с неожиданной  стороны.

Гравюра «Меланхолия» — обратите внимание на квадрат в правом верхнем углу:

 

 

 

 

 

 

 

 

 

Вот он крупнее:

 

 

 

 

 

 

 

 

 

Суть всех «магический квадратов» в общем-то понятна: сумма по столбикам и диагоналям равна какому-нибудь числу. Так и здесь. Это число 34. Но дело в том, что это число появляется при абсолютно ЛЮБОМ раскладе. Сумма левого верхнего квадрата — 34, то же самое верно в отношении правого верхнего, правого нижнего и левого нижнего малых квадратов. А также центрального квадрата — 10+11+6+7=34. А также, если сложить угловые цифры 16,13, 4 и 1, тоже получится 34.

А еще, если начать прокладывать линию от 1 до 16, то получится вот такая абсолютно симметричная (при чем и в зеркальном отношении!!) фигура:

А еще в самом низу числа 15 и 14 указывают на дату создания гравюры — 1514 год. А цифры в нижних углах —  4 и 1 — цифровые обозначения инициалов художника: D А — Дюрер Альбрехт.

Вся эта математическая «хиромантия» по мнению некоторых указывает на то, что Дюрер создавал свой квадрат не методом тыка или подбора, а с помощью других измерений. В смысле — выйдя за пределы 3-х измерений и ….  как-то на семимерном(????) уровне?….  Возможно, с помощью т.н. «конхоиды» или «раковины», как ее называл Дюрер (в своей математической монографии «Руководство по измерению циркулем и линейкой», вышедшее в 1525 г.) и автором которой являлся, он и создавал свой «магический квадрат».

 

 

 

 

«Конхоида»:

 

 

 

 

 

 

 

 

И обратите внимание на камень на гравюре — усеченный с двух углов паралеллепипед, боковыми гранями которого являются 2 правильных треугольника и 6 пятиугольников:

 

 

 

 

 

 

 

 

Роберт Лэнгдон, символист-детектив в книге «Утраченный символ» Дэна Брауна, накладывает 16-ти значный шифр из основания масонской пирамиды на квадрат Дюрера и получает расшифровку:

то есть  JEOVA SANCTUS UNUS — Единый Истинный Бог.

 

 

 

Дюрер по всей вероятности принадлежал к некому Тайному Обществу. И, возможно, обладал неким тайным сакральным знанием…

А, может, это все мистификация?!..

Давайте начертим 16 клеточек и проставим в них числа от 1 до 16 по порядку.  А теперь просто поменяйте местами 1 и 16, 4 и 13 (это углы), 6 и 10 и 7 и 11 (квадрат в середине). И еще стоящие рядом 2 и 3 и 14 и 15.

ВУАЛЯ! Вот он магический квадрат наикрутейшей степени. Просто? Просто! Но ведь еще поди догадайся, что и как менять.. С другой стороны, абсолютная симметрия замены чисел не может не наводить на мысль о простоте и универсальности решения. Или это нам сейчас легко рассуждать, а Дюреру понадобилось воспользоваться своей конхоидой (см. выше), чтобы понять, как и что менять местами?…

Невооруженным глазом видно исправление на гравюре, которое Дюрер НАМЕРЕННО оставил таким очевидным:

При замене чисел в нарисованном нам квадрате с 1 до 16 по порядку неизменными остаются только боковые 5 и 9 слева и 8 и 12 справа. Изначально Дюрер, хотел и их тоже поменять местами, но это оказалось не нужным. Зачем он оставил свою ошибку на всеобщее обозрение? Показать работу своей мысли? Тщеславие? А год 1514, так удачно вписавшийся в квадрат — тоже заслуга или художник для пущего эффекта просто подождал нужной даты, всю математику продумав раньше?))

Может и так. Даже сферы высшей математики возможно объяснить тщеславием художника, считавшего себя красавцем и регулярно писавшего свои автопортреты, чтобы им все могли любоваться.

Возвращаясь к «Меланхолии», магическим квадратам и оккультизму. Гравюра была написана для императора Максимилиана I (для тех, кто знает — мужа Марии Бургундской, зятя Карла Смелого и деда императора Карла V).

Вот его портрет тоже работы Дюрера:

Максимилиан считал себя меланхоликом. В средние века (да и сейчас) считалось, что меланхолики находятся под влиянием планеты Сатурн. Магический квадрат должен был быть неким талисманом, который отгонял бы мрачное влияние Сатурна, одновременно привлекая более положительную энергетику Юпитера.

В общем, писать про эту гравюру можно много. Можно еще все атрибуты рассмотреть — но это в другой раз. Математика показалась в данном случае мне более интересной, чем живопись.

 

 

 

 

Единичный квадрат — Википедия

Материал из Википедии — свободной энциклопедии

Единичный квадрат — квадрат, стороной которого является единичный отрезок. Единичный квадрат является единицей измерения площади. Иногда требуют, чтобы в прямоугольных координатах левый нижний угол единичного квадрата находился бы в начале координат и его стороны были бы параллельны осям координат. В этом случае его вершины имеют координаты (0,0){\displaystyle (0,0)}, (1,0){\displaystyle (1,0)}, (1,1){\displaystyle (1,1)} и (0,1){\displaystyle (0,1)}.

Часто под единичным квадратом подразумевается любой квадрат со стороной 1.

Если задана прямоугольная система координат, то этот термин часто используют в более узком смысле: единичный квадрат — это множество точек, обе координаты которых (x и y) лежат между 0 и 1:

{0≤x≤10≤y≤1{\displaystyle {\begin{cases}0\leq x\leq 1\\0\leq y\leq 1\end{cases}}}.

Иными словами, единичный квадрат — это прямое произведение I × I, где I — единичный отрезок [0;1]{\displaystyle [0;1]}.

В комплексной плоскости под единичным квадратом подразумевается квадрат с вершинами 0, 1, 1 + i и i^[1].

Единичный квадрат является единицей измерения площади фигуры. Измерить площадь фигуры — значит найти отношение площади фигуры к площади единичного квадрата, то есть сказать, сколько раз единичный квадрат может быть уложен в данной фигуре^[2]. Есть все основания предполагать, что так определяли площадь математики Древнего Вавилона^[3]. В «Началах» Евклида не было единицы измерения длины, а значит, не было понятия единичный квадрат. Евклид не измерял площади числами, вместо этого он рассматривал отношения площадей друг к другу^[4].

• Площадь единичного квадрата равна 1, периметр — 4, диагональ — 2{\displaystyle {\sqrt {2}}}.
• Единичный квадрат является «кругом» диаметра 1 в смысле равномерной нормы (L∞{\displaystyle L^{\infty }}), то есть множество точек, которые расположены на расстоянии 1/2 в смысле равномерной нормы от центра с координатами (1/2, 1/2), является единичным квадратом^[5].
• Кантор доказал, что существует взаимнооднозначное соответствие между единичным отрезком и единичным квадратом. Этот факт настолько противоречит интуиции, что Кантор в 1877 году писал Дедекинду: «Я вижу это, но не верю»^[6][7].
• Ещё более удивительный факт был открыт Пеано в 1890 году: оказывается существует непрерывное отображение отрезка на квадрат. Примером такого отображения является кривая Пеано, первый пример заполняющей пространство кривой. Кривая Пеано задаёт непрерывное отображение единичного отрезка на квадрат, так, что для каждой точки квадрата найдется соответствующая точка отрезка^[8].
• Тем не менее, не существует взаимнооднозначного непрерывного отображения отрезка в квадрат. Кривая Пеано содержит кратные точки, то есть она проходит через некоторые точки квадрата более одного раза. Таким образом, кривая Пеано не задаёт взаимнооднозначного соответствия. В действительности легко доказать, что отрезок не гомеоморфен квадрату, значит, избежать кратных точек невозможно^[9].

Неизвестно (на 2011 год), существует ли точка на плоскости такая, что расстояние до любой вершины единичного квадрата является рациональным числом. Однако известно, что такой точки не существует на границе квадрата^[10][11].

1. ↑ Weisstein, Eric W. Unit Square (англ.) на сайте Wolfram MathWorld.
2. ↑ Валерий Гусев, Александр Мордкович. Математика: учебно-справочное пособие. — Litres, 2016-06-10. — С. 436. — 674 с. — ISBN 9785457404793.
3. ↑ Peter Strom Rudman. How Mathematics Happened: The First 50,000 Years. — Prometheus Books, 2007-01-01. — С. 108. — 316 с. — ISBN 9781615921768.
4. ↑ Saul Stahl. Geometry from Euclid to Knots. — Courier Corporation, 2012-05-23. — С. 99-100. — 481 с. — ISBN 9780486134987.
5. ↑ Athanasios C. Antoulas. Approximation of Large-Scale Dynamical Systems. — SIAM, 2009-06-25. — С. 29. — 489 с. — ISBN 9780898716580.
6. ↑ Сергей Деменок. Фрактал: между мифом и ремеслом. — Litres, 2016-06-08. — С. 156. — 298 с. — ISBN 9785040137091.
7. ↑ Michael J. Bradley. The Foundations of Mathematics: 1800 to 1900. — Infobase Publishing, 2006. — С. 104—105. — 177 с. — ISBN 9780791097212.
8. ↑ Сергей Сизый. Математические задачи. Студенческие олимпиады математико-механического факультета Уральского госуниверситета. — Litres, 2016-04-14. — С. 34. — 128 с. — ISBN 9785040047086.
9. ↑ Александр Шень, Николай Верещагин. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств. — Litres, 2015-11-13. — С. 19. — 113 с. — ISBN 9785457918795.
10. ↑ Guy, Richard K. (1991), Unsolved Problems in Number Theory, Vol. 1 (2nd ed.), Springer-Verlag, с. 181—185 .
11. ↑ Barbara, Roy (March 2011), «The rational distance problem», Mathematical Gazette Т. 95 (532): 59—61, <http://journals.cambridge.org/action/displayAbstract?fromPage=online&aid=9458155> .

Полный квадрат — Википедия

Материал из Википедии — свободной энциклопедии

Полный квадрат, или квадратное число, — число, являющееся квадратом некоторого целого числа. Иными словами, квадратом является целое число, квадратный корень из которого извлекается нацело. Геометрически такое число может быть представлено в виде площади квадрата с целочисленной стороной.

Например, 9 — это квадратное число, так как оно может быть записано в виде 3 × 3, а также представляет площадь квадрата со стороной, равной 3.

Квадратное число входит в категорию классических фигурных чисел.

Последовательность квадратов начинается так:

0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, … (последовательность A000290 в OEIS)

Таблица квадратов

	_0	_1	_2	_3	_4	_5	_6	_7	_8	_9
0_	0	1	4	9	16	25	36	49	64	81
1_	100	121	144	169	196	225	256	289	324	361
2_	400	441	484	529	576	625	676	729	784	841
3_	900	961	1024	1089	1156	1225	1296	1369	1444	1521
4_	1600	1681	1764	1849	1936	2025	2116	2209	2304	2401
5_	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6_	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
7_	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8_	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9_	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Квадрат натурального числа n{\displaystyle n} можно представить в виде суммы первых n{\displaystyle n} нечётных чисел:

1: 1=1{\displaystyle 1=1}

2: 4=1+3{\displaystyle 4=1+3}

…

7: 49=1+3+5+7+9+11+13{\displaystyle 49=1+3+5+7+9+11+13}

…

Ещё один способ представления квадрата натурального числа:
n2=1+1+2+2+…+(n−1)+(n−1)+n{\displaystyle n^{2}=1+1+2+2+…+(n-1)+(n-1)+n}
Пример:

1: 1=1{\displaystyle 1=1}

2: 4=1+1+2{\displaystyle 4=1+1+2}

…

4: 16=1+1+2+2+3+3+4{\displaystyle 16=1+1+2+2+3+3+4}

…

Сумма квадратов первых n{\displaystyle n} натуральных чисел вычисляется по формуле^[1]:

∑k=1nk2=12+22+32+…+n2=n(n+1)(2n+1)6{\displaystyle \sum _{k=1}^{n}k^{2}=1^{2}+2^{2}+3^{2}+…+n^{2}={\frac {n(n+1)(2n+1)}{6}}}

Вывод

Способ 1, метод приведения:

Рассмотрим сумму кубов натуральных чисел от 1 до n+1{\displaystyle n+1}:

∑k=1nk3+(n+1)3=∑k=0n(k+1)3=∑k=0n(k3+3k2+3k+1)=∑k=0nk3+∑k=0n3k2+∑k=0n3k+∑k=0n1=∑k=0nk3+3∑k=0nk2+3∑k=0nk+∑k=0n1{\displaystyle \sum _{k=1}^{n}k^{3}+(n+1)^{3}=\sum _{k=0}^{n}(k+1)^{3}=\sum _{k=0}^{n}(k^{3}+3k^{2}+3k+1)=\sum _{k=0}^{n}k^{3}+\sum _{k=0}^{n}3k^{2}+\sum _{k=0}^{n}3k+\sum _{k=0}^{n}1=\sum _{k=0}^{n}k^{3}+3\sum _{k=0}^{n}k^{2}+3\sum _{k=0}^{n}k+\sum _{k=0}^{n}1}

Получим:

(n+1)3=3∑k=0nk2+3∑k=0nk+∑k=0n1=3∑k=0nk2+3(n+1)n2+(n+1){\displaystyle (n+1)^{3}=3\sum _{k=0}^{n}k^{2}+3\sum _{k=0}^{n}k+\sum _{k=0}^{n}1=3\sum _{k=0}^{n}k^{2}+3{\frac {(n+1)n}{2}}+(n+1)}

Умножим на 2 и перегруппируем:

6∑k=0nk2=2(n+1)3−3(n+1)n−2(n+1)=(n+1)(2(n+1)2−3n−2)=(n+1)(2n2+n)=n(n+1)(2n+1){\displaystyle 6\sum _{k=0}^{n}k^{2}=2(n+1)^{3}-3(n+1)n-2(n+1)=(n+1)(2(n+1)^{2}-3n-2)=(n+1)(2n^{2}+n)=n(n+1)(2n+1)}

∑k=0nk2=n(n+1)(2n+1)6{\displaystyle \sum _{k=0}^{n}k^{2}={\frac {n(n+1)(2n+1)}{6}}}       (В рассуждениях использована формула: ∑k=0nk=(n+1)n2{\displaystyle \sum _{k=0}^{n}k={\frac {(n+1)n}{2}}}, вывод которой аналогичен приведенному)

Способ 2, метод неизвестных коэффициентов:

Заметим, что сумма функций степени N{\displaystyle N} может быть выражена как функция N+1{\displaystyle N+1} степени. Исходя из этого факта предположим:

∑k=0nk2=f(n)=An3+Bn2+Cn+D{\displaystyle \sum _{k=0}^{n}k^{2}=f(n)=An^{3}+Bn^{2}+Cn+D}

f(0)=0;f(1)=1;f(2)=5;f(3)=14{\displaystyle f(0)=0;f(1)=1;f(2)=5;f(3)=14}

Получим систему линейных уравнений относительно искомых коэффициентов:

{0A+0B+0C+D=0A+B+C+D=18A+4B+2C+D=527A+9B+3C+D=14{\displaystyle {\begin{cases}0A+0B+0C+D=0\\A+B+C+D=1\\8A+4B+2C+D=5\\27A+9B+3C+D=14\\\end{cases}}}

Решив её, получим A=13,B=12,C=16,D=0{\displaystyle A={\frac {1}{3}},B={\frac {1}{2}},C={\frac {1}{6}},D=0}

Таким образом:

∑k=0nk2=f(n)=13n3+12n2+16n+0=n(n+1)(2n+1)6{\displaystyle \sum _{k=0}^{n}k^{2}=f(n)={\frac {1}{3}}n^{3}+{\frac {1}{2}}n^{2}+{\frac {1}{6}}n+0={\frac {n(n+1)(2n+1)}{6}}}

Ряд обратных квадратов сходится^[2]:

∑n=1∞1n2=112+122+⋯+1n2+⋯=π26{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+\dots +{\frac {1}{n^{2}}}+\dots ={\frac {\pi ^{2}}{6}}}

Четыре различных квадрата не могут образовывать арифметическую прогрессию.^[3] Арифметические прогрессии из трёх квадратов существуют — например: 1, 25, 49.

Каждое натуральное число может быть представлено как сумма четырёх квадратов (теорема Лагранжа о сумме четырёх квадратов).

4900 — единственное число > 1, которое является одновременно квадратным и пирамидальным.

Суммы пар последовательных треугольных чисел являются квадратными числами.

В десятичной записи квадратные числа имеют следующие свойства:

• Последняя цифра квадрата в десятичной записи может быть равной 0, 1, 4, 5, 6 или 9 (квадратичные вычеты по модулю 10).
• Квадрат не может оканчиваться нечётным количеством нолей.
• Квадрат либо делится на 4, либо при делении на 8 даёт остаток 1. Квадрат либо делится на 9, либо при делении на 3 даёт остаток 1.
• Две последние цифры квадрата в десятичной записи могут принимать значения 00, 01, 04, 09, 16, 21, 24, 25, 29, 36, 41, 44, 49, 56, 61, 64, 69, 76, 81, 84, 89 или 96 (квадратичные вычеты по модулю 100). Зависимость предпоследней цифры квадрата от последней можно представить в виде следующей таблицы:

последняя цифра	предпоследняя цифра
0	0
5	2
1, 4, 9	чётная
6	нечётная

1

• Виленкин Н. Я., Шибасов Л. П. Шибасова 3. Ф. За страницами учебника математики: Арифметика. Алгебра. Геометрия. — М.: Просвещение, 1996. — С. 30. — 320 с. — ISBN 5-09-006575-6.
• Деза Е., Деза М. Фигурные числа. — М.: МЦНМО, 2016. — 349 с. — ISBN 978-5-4439-2400-7.